Hình thoi có tên tiếng Anh là Rhombus là một tứ giác có 4 cạnh bằng nhau nhìn khá giống hình vuông. Và một trong những điểm băn khoăn mà các học sinh hiện nay thường hay gặp phải khi tiếp xúc với hình thoi đó là cách tính chu vi, cách tính diện tích hình thoi. Dưới đây, chúng tôi sẽ giải đáp những thắc mắc trên một cách cụ thể nhất..
Hình thoi là gì?
Hình thoi là một tứ giác mà bốn cạnh của tứ giác bằng nhau. Là hình bình hành có hai cạnh kề bằng nhau hoặc hình bình hành có hai đường chéo vuông góc.
Tính chất của hình thoi
- 2 góc đối diện bằng nhau
- 2 đường chéo vuông góc với nhau và cắt nhau ở giữa mỗi đường thẳng
- 2 đường chéo là được coi là tia phân giác của góc.
- Hình thoi là hình có tất cả các tính chất của hình bình hành.
- Hai đường chéo là đường phân giác hình thoi.
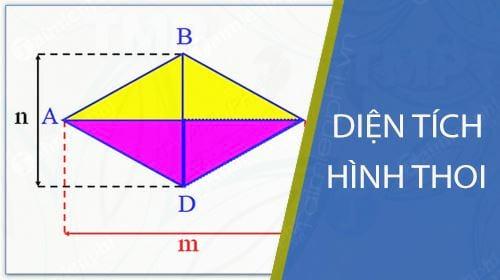
Dấu hiệu nhận biết hình thoi:
- Có 4 cạnh bằng nhau.
- Một hình bình hành có hai cạnh đồng dư kề nhau.
- Hình bình hành có hai đường chéo mà nó vuông góc với nhau.
- Hình bình hành có đường chéo mà nó là tia phân giác của một góc.
Công thức tính chu vi hình thoi dễ hiểu
– Khái niệm về công thức tính chu vi hình thoi: được tính bằng tổng độ dài của các đường bao quanh hình thoi và đó cũng là đường bao quanh toàn bộ diện tích.
– Công thức tính:
Tính chu vi hình thoi khi biết độ dài của cạnh:
Cũng giống như công thức tính chu vi của hình vuông, hình thoi cũng có cách tính như sau:
P = a x 4
Trong đó:
– P là chu vi hình thoi
– a là độ dài cạnh hình thoi
Công thức trên được phát biểu bằng lời như sau: Chu vi của hình thoi bằng độ dài một cạnh nhân với 4 hoặc bằng 4 lần độ dài một cạnh hình thoi.
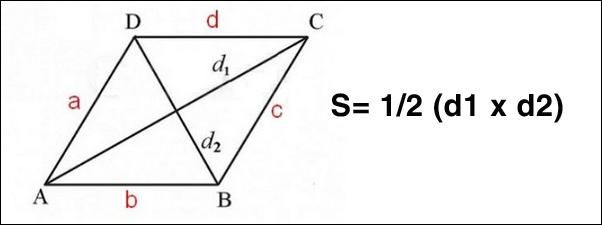
Ví dụ 1: Tính chu vi của hình thoi biết độ dài cạnh = 10 cm.
Giải: Áp dụng công thức tính chu vi của hình thoi, ta có:
Chu vi hình thoi đó là: 10 x 4 = 40 (cm)
Ví dụ 2: Dựa vào hướng dẫn bài trên, hãy tính chu vi của hình thoi, biết độ dài cạnh lần lượt là:
a) 8 cm b) 11 dm c) 3/4 cm d) 2,5 m
Giải:
a) Chu vi của hình thoi là: 8 x 4 = 32 (cm)
b) Chu vi của hình thoi là: 11 x 4 = 44 (dm)
c) Chu vi của hình thoi là: 3/4 x 4 = 4 (cm)
d) Chu vi của hình thoi là: 2,5 x 4 = 10 (m)
Tính chu vi hình thoi khi đã biết diện tích, độ dài 2 đường chéo hình thoi
* Tính đường chéo hình thoi khi biết diện tích và độ dài 1 đường chéo hình thoi:
Nếu đã biết diện tích hình thoi, độ dài đường chéo (d1), khi đó chúng ta sẽ dễ dàng tìm được 1 đường chéo còn lại của hình thoi theo cách tính sau: d2 = 2S/ d1.
Phương pháp giải: Áp dụng công thức tính diện tích và chu vi hình thoi theo đó: P = a x 4 và S = 1/2 x d1 x d2
Ví dụ 3: Tính chu vi hình thoi biết các đường chéo bằng 16cm và 30cm
Gọi cạnh hình thoi bằng a và các đường chéo của hình thoi lần lượt là d1 và d2
Ta áp dụng định lý Py-ta-go trong tam giác vuông, theo đó bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông ta có như sau: a2 = (d1/2)2 + (d2/2)2= (8)2 + (15)2 hay a = 17
Như vậy chu vi hình thoi: P = 4 x a = 68.
Tính diện tích hình thoi bằng công thức nào là nhanh nhất?
– Khái niệm diện tích hình thoi: được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng có thể nhìn thấy của hình thoi.
– Các công thức tính diện tích hình thoi theo từng trường hợp:
Công thức tính diện tích hình thoi khi biết cạnh đáy và chiều cao hình thoi
Diện tích của hình thoi được tính bằng một nửa tích độ dài của hai đường chéo hình thoi, công thức như sau:
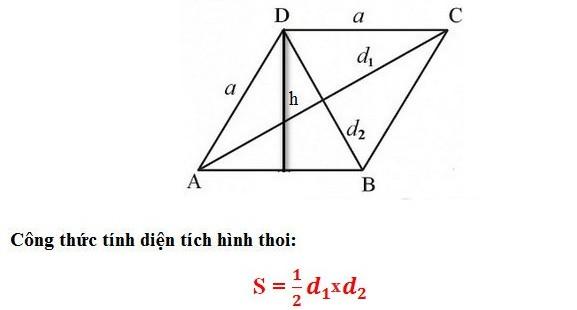
Trong đó:
- S là diện tích hình thoi.
- d1 và d2 là hai đường chéo hình thoi.
Ví dụ về cách diện tích hình thoi.
Ví dụ: Có một tấm bìa cactong hình thoi đo được hai đường chéo cắt nhau có chiều dài lần lượt là 8cm và 10 cm. Hỏi diện tích của tấm bìa bằng hình thoi đó bằng bao nhiêu?
Áp dụng theo công thức tính diện tích hình thoi, ta có d1 = 8 cm và d2 = 10 cm. Ta đưa vào công thức và có kết quả như sau:
S = 1/2 x (d1 x d2) = 1/2 (8 x 10) = 1/2 x 80 = 40 cm2
Cách tính diện tích hình thoi dựa vào hệ thức trong tam giác (Nếu biết góc của hình thoi)
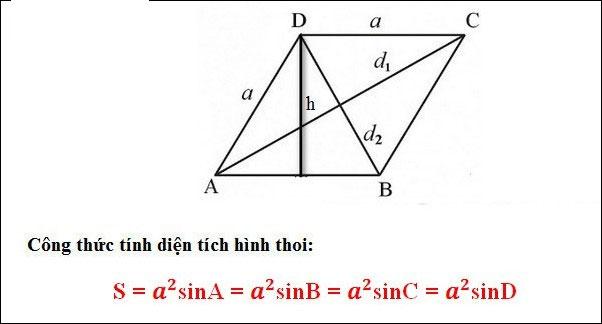
Biết, a là cạnh của hình thoi
Ví dụ 1: Cho hình thoi ABCD như hình trên, có cạnh hình thoi = 4dm, góc A = 35 độ. Tính diện tích hình thoi ABCD.
Phương pháp giải: Áp dụng công thức, ta có a = 4, góc = 35 độ. Ta thay vào công thức như sau:
S = a2 x sinA = 42 x sin(35) = 9,176 (dm2)
Phương pháp vẽ hình thoi chuẩn, đơn giản nhất
Cách 1 : Vẽ hình thoi ABCD bằng cách dùng thước kẻ và êke
Bước 1: Vẽ đoạn thẳng AC bất kì và xác định trung điểm O của đoạn thẳng đã vẽ.
Bước 2: Dùng êke vẽ đoạn thẳng BD vuông góc với đoạn AC tại O và nhận trung điểm O là trung điểm của đoạn BD.
Bước 3: Nối các đỉnh A với B, B với C, C với D, D với A ta được hình thoi ABCD.
Cách 2 : Vẽ hình thoi bằng compa và thước kẻ
Bước 1: Vẽ đoạn thẳng AC.
Bước 2: Dùng compa tiến hành mở rộng độ mở compa lớn hơn 1/2 AC. Vẽ cung tròn có tâm A và tâm C sao cho hai cung tròn đó cắt nhau tại hai điểm, hai giao điểm này gọi lần lượt được gọi là B và D.
Bước 3: Nối các điểm A, B, C, D vừa tạo thành ở các bước trên với nhau ta được hình thoi ABCD.
Như vậy, trên đây chúng tôi đã đưa ra những giải đáp về thắc mắc liên quan đến cách tính diện tích hình thoi, chu vi hình thoi dễ hiểu nhất. Ngoài ra để tiện hơn trong quá trình tính toán, chúng tôi cũng cung cấp một số cách vẽ hình thoi ABCD sao cho đơn giản mà chính xác nhất.











